[掃雷]分析法差之毫釐 - 你以為的線性真的正確嗎？

我們常用來尋找兩個變數的關聯方法有兩種 -- 相關係數或迴歸分析。這兩者的基礎都是線性！這是因為我們將線性視為最能表現趨勢方向的指標，所以在經濟學或是股市分析上常以直線來表述長期趨勢。

我們也以這條直線將數據區分出長期趨勢與短期波動。在股市分析上就是長期價值投資與短線操作。

為什麼使用線性的方法來幫助我們判別趨勢呢？

原因非常簡單。那就是直覺，好用，易懂。這是人的本性，所以才會採用這樣的方法。另外一個原因則是數據如果走勢是彎曲，很可能因為找不出最適的非線性方程式，就此算了。所以，最終還是常用直線表示趨勢。

使用直線時卻會遭遇到的問題

第一個問題你抓不住短期波動，或是搞短線容易失敗。為了解決第一個問題，非常豐富的期刊論文都在討論這個議題，並且試圖使用各種方法討論波動性如何被捕捉。那麼我們就得繼續深入問問題了！

這個波動性產生的前提是什麼？看到這邊，朋友們都知道了吧？來自直線！可如果我們可以配適非線性模式呢？試問這波動性會不會改變？直覺而論，這是當然會改變的！所以我們討論波動性是有其前提的，而且這個前提還是可以被改變的，不是真理！

那麼當大多數的人將前提當做永恆的真理時，也有眾多的論證，孰能忍受原來前提是可被改變的事情呢！但對於數據分析師而言，這就是回到科學的意義 -- 求真、求實。

第二個問題，你繪製的直線是根據樣本個數所決定的，不代表接下來仍符合這樣的趨勢，或是你將樣本個數增加，例如使用更多的歷史資料，那就很可能線型改變。所以這第二個問題就會延伸出次問題：多少樣本個數才足夠？這跟資料量多少才叫做大數據有著異曲同工之妙。被視為理所當然，或是不認為這樣的問題是重要的，就會導致現在的問題始終不曾消失。

事實

讓我在這邊簡單說明兩者的問題點吧，就用簡單迴歸模型說明。當我有一個自變數(X)與應變數(Y)，所以我們很容易就將兩者的關係用直線型表示，

                                                                (1)

b0是截距，b1是斜率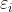，是誤差，n為樣本個數。可實際上兩者的關係真的是線性關係嗎？沒有人知道，因為那是我們自己認定的。所以兩者的關係應該是這樣才對。

                                                                           (2)

我們不知道這個函數的形式，所以用H(‧)代表。因此，我們需要找出H(‧)的形式[註1]。在多個自變數下一樣也是如此。不過這個觀念不是迴歸分析一開始就如此。這也就是我們在學習過程中，已經先用直線框住思維，當有偏誤發生再來討論解決問題。可是這個偏誤就是一開始的模式設定錯誤，自然不可能再用偏誤去導正。因此在課本上就形成了一個「誤用」章節來進行說明。

觀念

那麼我在這要說明一個觀念：模型的模式設定錯誤的錯誤，進入殘差是無法被消除的。這是很多人都沒有注意到，或者認為影響微乎其微就算了的問題點。我就用前述的(1)和(2)來說明。我先假設H(‧)包含指數函數的形式，所以(2)就是

這種模式不是取log就還原。此時你用線性模式估計就會造成模型設定錯誤，並且這個錯誤會出現在殘差裡面。這時候的殘差不具有誤差的代表性，但這點卻無法被檢測出來。而且會影響變異數異質性(Heteroskedasticity)和序列相關的影響程度。對此，在統計學、迴歸分析與計量經濟學皆是無解的問題。

可是當你要做精準分析時，就不能妥協在過去的分析方法上，而是要將這些問題解決。因此，我提出「你以為線性模式就是正確嗎？」的問題。這個問題或許很多人會認為大家都有討論過，或許是我所見不足廣泛，過去沒有見過解答。所以，認真思考後，如果理論是正確的，那為什麼數據分析如此困難，方法千奇百怪。那如果數據是正確的，那麼我是否應該調整對數據分析的看法，從數據特性開始分析，而非我個人的主觀認定模型出發。

據此理，我們就應隨著數據的特性去配出模型，而不是用主觀認定去套用在數據上。這個觀念人人都懂，但深陷其中後，卻好似遺忘。這就像我們常說「適性發展」，但最終還是套了一個模子在人的身上。

註1：計量經濟學教科書當中都會提到模式設定錯誤會造成偏誤發生。其實實際狀況很多資料之間的關係並非簡單的直線就能表示。所以教科書當中亦有提及幾個常用的數學模式，實則步足夠的。另外，如果你執行變數轉換，那也要能讓數據還原。可參考時間序列模型與數據要求條件，然後試著推導看看，用估計線還原應變數形式。